(ENEM 2019) Construir figuras de diversos tipos, apenas dobrando e cortando papel, sem cola e sem tesoura, é a arte do origami (ori = dobrar; kami = papel), que tem um significado altamente simbólico no Japão. A base do origami é o conhecimento do mundo por base do tato. Uma jovem resolveu construir um cisne usando a técnica do origami, utilizando uma folha de papel de 18 cm por 12 cm. Assim, começou por dobrar a folha conforme a figura.
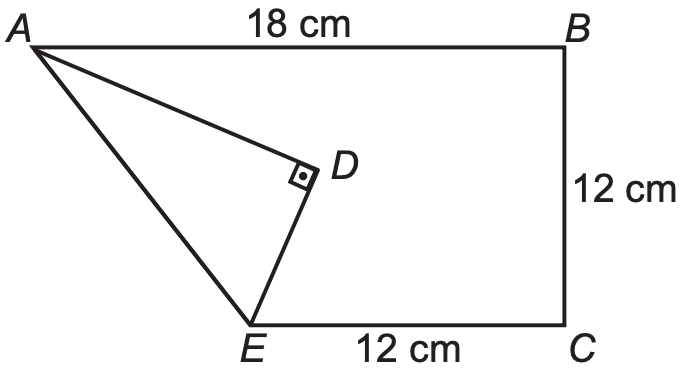
Após essa primeira dobradura, a medida do segmento AE é
A) \(2\sqrt{22} cm.\)
B) \(6\sqrt{3} cm.\)
C) \(12 cm.\)
D) \(6\sqrt{5} cm.\)
E) \(12\sqrt{2} cm.\)
Dicas e Resolução
Dica 1
Dica 2
Dica 3
Dica 4
Resolução da Dica 4
Resposta: Alternativa D
Resolução por escrito
Vamos começar desenhando o papel original, apenas com a marquinha da dobra.

Pela imagem, a gente sabe que a largura do retângulo vale 18 cm. Então, o segmento DC vale 18 cm. Pela figura também, sabemos que EC vale 12 cm. Logo, o segmento DE vale 18 – 12 = 6 cm.

A gente sabe também, pela imagem, que a altura do retângulo vale 12 cm. Logo AD vale 12 cm.
Agora, se você reparar bem, nós temos o triângulo retângulo ADE na figura. E basta aplicar o teorema de Pitágoras para encontrar o valor de AE.
\(AE^2 = 12^2 + 6^2\)
\(\iff AE^2 = 144 + 36\)
\(\iff AE^2 = 180\)
\(\iff AE = \sqrt{180}\)
\(\iff AE = \sqrt{9\times4\times5}\)
\(\iff AE = \sqrt{3^2\times2^2\times5}\)
\(\iff AE = 3\times2\times\sqrt{5} = 6\sqrt{5}\)
\(\iff AE = 6\sqrt{5}\)
Resposta
Alternativa D
Resolução ENEM 2019 – Matemática e suas Tecnologias
Acesse aqui a resolução detalhada da prova do ENEM 2019 – Matemática e suas Tecnologias
Como foi a sua experiência?
Links Relacionados
Lista de exercícios resolvidos, divididos por assunto e nível de dificuldade
O Desafio está lançado
Quero te fazer um Desafio: resolver pelo menos um exercício de matemática por dia, até a data do ENEM. Você aceita o Desafio? Sem sim, cadastre o seu email abaixo e você estará inscrito no Desafio. Esse será um treinamento muito bom para você chegar bem preparado no ENEM.



