(UFRN 2012 Vagas Remanescentes) Em um dia tumultuado na Bolsa de Valores, o valor, em reais, de cada ação de uma empresa variou conforme a função P(k) = 45 + 27.cos(k), sendo k um número real positivo. De acordo com a função apresentada, cada ação dessa empresa atingiu, nesse dia, o valor mínimo de
A) R$ 27,00. B) R$ 15,00. C) R$ 18,00. D) R$ 45,00.
(ENEM 2017) Um cientista, em seus estudos para modelar a pressão arterial de uma pessoa, utiliza uma função do tipo \(P(t)=A+Bcos(kt)\) em que \(A\), \(B\) e \(k\) são constantes reais positivas e \(t\) representa a variável tempo, medida em segundo. Considere que um batimento cardíaco representa o intervalo de tempo entre duas sucessivas pressões máximas.
Ao analisar um caso específico, o cientista obteve os dados:

A função \(P(t)\) obtida, por este cientista, ao analisar o caso específico foi
A) \(P(t)=99+21cos(3 \pi t)\)
B) \(P(t)=78+42cos(3 \pi t)\)
C) \(P(t)=99+21cos(2 \pi t)\)
D) \(P(t)=99+21cos(t)\)
E) \(P(t)=78+42cos(t)\)
(ENEM 2015 PPL) Um técnico precisa consertar o termostato do aparelho de ar-condicionado de um escritório, que está desregulado. A temperatura T, em graus Celsius, no escritório, varia de acordo com a função \(T(h)=A+Bsen(\frac{\pi}{12}(h-12))\), sendo h o tempo, medido em horas, a partir da meia-noite \((0 \le h < 24)\) e A e B os parâmetros que o técnico precisa regular. Os funcionários do escritório pediram que a temperatura máxima fosse 26°C, a mínima 18°C, e que durante a tarde a temperatura fosse menor do que durante a manhã.
Quais devem ser os valores de A e de B para que o pedido dos funcionários seja atendido?
A A = 18 e B = 8
B A = 22 e B = -4
C A = 22 e B = 4
D A = 26 e B = -8
E A = 26 e B = 8
(ENEM 2014 PPL) Uma pessoa usa um programa de computador que descreve o desenho da onda sonora correspondente a um som escolhido. A equação da onda é dada, num sistema de coordenadas cartesianas, por y = a · sen[b(x + c)], em que os parâmetros a, b, c são positivos. O programa permite ao usuário provocar mudanças no som, ao fazer alterações nos valores desses parâmetros. A pessoa deseja tornar o som mais agudo e, para isso, deve diminuir o período da onda.
O(s) único(s) parâmetro(s) que necessita(m) ser alterado(s) é(são)
A a.
B b.
C c.
D a e b.
E b e c.
(UFRN 2010) Considere a figura abaixo, na qual a circunferência tem raio igual a 1.

Nesse caso, as medidas dos segmentos ON, OM e AP, correspondem, respectivamente, a
A) senx, secx e cotgx.
B) cosx, senx e tgx.
C) cosx, secx e cossecx.
D) tgx, cossecx e cosx.
(ENEM 2009) Considere um ponto P em uma circunferência de raio r no plano cartesiano. Seja Q a projeção ortogonal de P sobre o eixo x, como mostra a figura, e suponha que o ponto P percorra, no sentido anti-horário, uma distância d ≤ r sobre a circunferência.
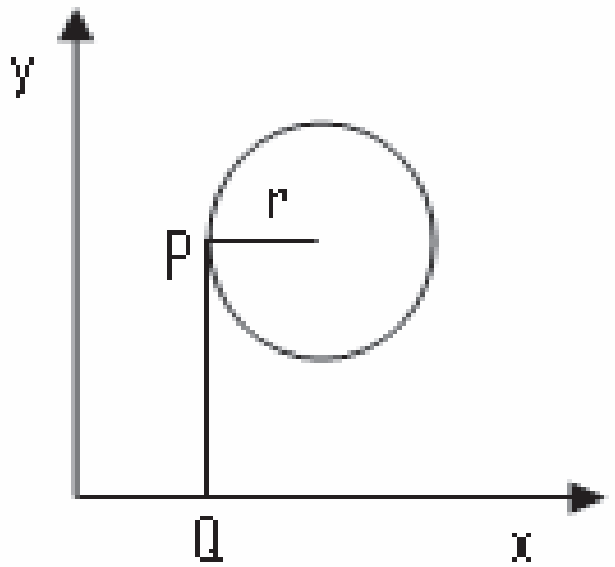
Então, o ponto Q percorrerá, no eixo x, uma distância dada por
A) \(r(1-sen \frac{d}{r})\)
B) \(r(1-cos \frac{d}{r})\)
C) \(r(1-tg \frac{d}{r})\)
D) \(rsen(\frac{r}{d})\)
E) \(rcos(\frac{r}{d})\)
(ENEM 2010) Um satélite de telecomunicações, t minutos após ter atingido sua órbita, está a r quilômetros de distância do centro da Terra. Quando r assume seus valores máximo e mínimo, diz-se que o satélite atingiu o apogeu e o perigeu, respectivamente. Suponha que, para esse satélite, o valor de r em função de t seja dado por
\(r(t)=\frac{5865}{1+0,15\times cos(0,06t)}\)
Um cientista monitora o movimento desse satélite para controlar o seu afastamento do centro da Terra. Para isso, ele precisa calcular a soma dos valores de r, no apogeu e no perigeu, representada por S.
O cientista deveria concluir que, periodicamente, S atinge o valor de
A) 12 765 km.
B) 12 000 km.
C) 11 730 km.
D) 10 965 km.
E) 5 865 km.
(FAMERP 2020) A figura indica os gráficos de uma reta r e uma senoide s, de equações \(y=\frac{5}{2}\) e y = 1 + 3 sen (2x), em um plano cartesiano de eixos ortogonais.

Sendo P um ponto de intersecção dos gráficos, conforme mostra a figura, sua abscissa, convertida para graus, é igual a
A) 275o
B) 240o
C) 225o
D) 210o
E) 195o
(ENEM 2015) Segundo o Instituto Brasileiro de Geografia e Estatística (IBGE), produtos sazonais são aqueles que apresentam ciclos bem definidos de produção, consumo e preço. Resumidamente, existem épocas do ano em que a sua disponibilidade nos mercados varejistas ora é escassa, com preços elevados, ora é abundante, com preços mais baixos, o que ocorre no mês de produção máxima da safra.
A partir de uma série histórica, observou-se que o preço P, em reais, do quilograma de um certo produto sazonal pode ser descrito pela função \(P(x)=8+5cos(\frac{\pi x – \pi}{6})\), onde x representa o mês do ano, sendo x = 1 associado ao mês de janeiro, x = 2 ao mês de fevereiro, e assim sucessivamente, até x = 12 associado ao mês de dezembro.
Disponível em: www.ibge.gov.br. Acesso em: 2 ago. 2012 (adaptado).
Na safra, o mês de produção máxima desse produto é
A janeiro.
B abril.
C junho.
D julho.
E outubro.


