Você está acessando o Passo 3 do nosso programa: Probabilidades e Análise Combinatória – Passo a Passo do Básico ao Avançado.
Árvore de Possibilidades
No Passo 3 iremos estudar um conceito muito importante: a Árvore de Possibilidades. Se você compreender bem a Árvore de Possibilidades, você já estará no caminho certo para saber resolver qualquer exercício de Análise Combinatória do ENEM. A seguir você terá uma série de exercícios, que vão te guiar passo a passo. Muito importante: tente resolver cada exercício por alguns minutos, antes de acessar os vídeos de dicas e resolução. A melhor maneira de você aprender matemática é resolvendo questões por conta própria.
Exercício 1
a) Há 2 lâmpadas em um lustre. Cada lâmpada pode estar ligada ou desligada. Qual o número total de configurações possíveis do lustre? Por exemplo, uma configuração possível é: a primeira lâmpada estar ligada, e a segunda lâmpada estar desligada. Outro exemplo de configuração seria a primeira lâmpada ligada, e a segunda também ligada.
Resposta: 2 × 2 = 4
b) Há 3 lâmpadas em um lustre. Cada lâmpada pode estar ligada ou desligada. Qual o número total de configurações possíveis do lustre? Por exemplo, uma configuração possível é: primeira lâmpada ligada, segunda lâmpada desligada e terceira lâmpada ligada.
Resposta: 2 × 2 × 2 = 8
c) Há 4 lâmpadas em um lustre. Cada lâmpada pode estar ligada ou desligada. Qual o número total de configurações possíveis do lustre?
Resposta: 2 × 2 × 2 × 2 = 16
d) Há 5 lâmpadas em um lustre. Cada lâmpada pode estar ligada ou desligada. Qual o número total de configurações possíveis do lustre?
Resposta: 2 × 2 × 2 × 2 × 2 = 32
e) A mesma questão com 6, 7 e 8 lâmpadas.
Resposta:
6 lâmpadas:
2 × 2 × 2 × 2 × 2 × 2 = 64
7 lâmpadas:
2 × 2 × 2 × 2 × 2 × 2 × 2 = 128
8 lâmpadas:
2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256
Exercício 2
2a) Zezinho está aprendendo a escrever. Ele já sabe escrever as letras “a” e “b”, e ainda não aprendeu as outras. Usando apenas as letras “a” e “b”, quantas palavras de 2 letras ele pode formar? Mesmo que a palavra não faça sentido. Por exemplo, ele pode formar a palavra “aa”, um outro exemplo seria a palavra “ba”.
Resposta: 2 × 2 = 4
2b) Usando apenas as letras “a” e “b”, quantas palavras de 3 letras Zezinho pode formar? Mesmo que a palavra não faça sentido.
Resposta: 2 × 2 × 2 = 8
2c) Usando apenas as letras “a” e “b”, quantas palavras de 4 letras Zezinho pode formar? Mesmo que a palavra não faça sentido.
Resposta: 2 × 2 × 2 × 2 = 16
2d) Usando apenas as letras “a” e “b”, quantas palavras de 5 letras Zezinho pode formar? Mesmo que a palavra não faça sentido.
Resposta: 2 × 2 × 2 × 2 × 2 = 32
2e) Usando apenas as letras “a” e “b”, quantas palavras de 6, 7 e 8 letras Zezinho pode formar? Mesmo que a palavra não faça sentido.
Resposta:
6 lâmpadas: 64
7 lâmpadas: 128
8 lâmpadas: 256
Exercício 3
3a) Uma lanchonete permite que você monte seu próprio sanduíche. O sanduíche é feito com pão e carne. Você pode escolher uma dentre 2 opções de pão: francês ou italiano. E uma dentre 3 opções de carne: contra filé, presunto ou rosbife. De quantas maneiras você pode montar o sanduíche?
Resposta: 2 × 3 = 6
3b) A lanchonete adicionou o sanduíche premium no cardápio. Esse sanduíche é feito de pão, carne e molho. Além das opções de pão e carne do item anterior, você também escolhe uma dentre 2 opções de molho: Maionese ou molho Tártaro. De quantas maneiras você pode montar o sanduíche premium?
Resposta: 2 × 3 × 2 = 12
3c) A lanchonete resolveu lançar o sanduíche master, que vem com pão, carne, molho e salada. As opções de pão, carne e molho são as mesmas dos itens anteriores. Além disso você escolhe uma dentre 2 opções de salada: Alface ou Rúcula. De quantas maneiras você pode montar o sanduíche master?
Resposta: 2 × 3 × 2 × 2 = 24
3d) A lanchonete agora está lançando o sanduíche completo, com pão, carne, molho, salada e queijo. As opções de pão, carne, molho e salada são as mesmas dos itens anteriores. Além disso você escolhe um dentre 3 tipos de queijo: Provolone, Ricota ou Minas. De quantas maneiras você pode montar o sanduíche completo?
Resposta: 2 × 3 × 2 × 2 × 3 = 72
Exercício 4
4a) Um restaurante oferece um menu de almoço, com entrada e prato principal. Eles têm 2 opções de entrada: Sopa ou Patê. E 4 opções de prato principal: Frango, Carne, Peixe ou Macarrão. De quantas maneiras podemos montar o menu de almoço, escolhendo uma entrada e um prato principal?
Resposta: 2 × 4 = 8
4b) O restaurante oferece também o menu especial, com entrada, prato principal e uma bebida. As opções de entrada e prato principal são as mesmas do item anterior. Além disso, você escolhe uma dentre 3 opções de bebida: Refrigerante, Suco ou Água. De quantas maneiras diferentes podemos montar o menu especial?
Resposta: 2 × 4 × 3 = 24
4c) No restaurante você também pode escolher o menu supremo, com entrada, prato principal, bebida e sobremesa. As opções de entrada e prato principal e bebida são as mesmas dos itens anteriores. Além disso, você escolhe uma dentre 3 opções de sobremesa: Sorvete, Bolo ou Torta. De quantas maneiras diferentes podemos montar o menu supremo?
Resposta: 2 × 4 × 3 × 3 = 72
4d) O restaurante tem também o menu completo, com entrada, prato principal, bebida, sobremesa e café. As opções de entrada e prato principal, bebida e sobremesa são as mesmas dos itens anteriores. Além disso, você escolhe uma dentre 2 opções de café: Expresso ou com Leite. De quantas maneiras diferentes podemos montar o menu completo?
Resposta: 2 × 4 × 3 × 3 × 2 = 144
Exercício 5
5a) Laurinha está aprendendo a escrever os números. Ela já sabe escrever os algarismos 1, 2 e 3, e ainda não aprendeu os outros. Usando apenas os algarismos 1, 2 e 3, quantos números de 2 dígitos ela consegue formar? Por exemplo, ela já pode escrever o número 111, outro exemplo seria o número 332.
Resposta: 3 × 3 = 9
5b) Usando apenas os algarismos 1, 2 e 3, quantos números de 3 dígitos Laurinha consegue formar?
Resposta: 3 × 3 × 3 = 27
5c) Usando apenas os algarismos 1, 2 e 3, quantos números de 4 dígitos Laurinha consegue formar?
Resposta: 3 × 3 × 3 × 3 = 81
5d) Usando apenas os algarismos 1, 2 e 3, quantos números de 5 dígitos Laurinha consegue formar?
Resposta: 3 × 3 × 3 × 3 × 3 = 243
Exercício 6
Uma lanchonete permite que você monte seu próprio sanduíche. Você pode escolher uma dentre 3 opções de pão: francês, italiano ou australiano. Uma dentre 4 opções de carne: contra filé, peito de peru, presunto ou rosbife. E uma dentre 2 opções de molho: Maionese ou Tártaro. De quantas maneiras você pode montar o sanduíche?
Resposta: 3 × 4 × 2 = 24
Universidade Estadual de Goiás 2015
(UEG 2015) Numa lanchonete o lanche é composto por três partes: pão, molho e recheio. Se essa lanchonete oferece aos seus clientes duas opções de pão, três de molho e quatro de recheio, a quantidade de lanches distintos que ela pode oferecer é de
a) 9
b) 12
c) 18
d) 24
Resposta: 2 × 3 × 4 = 24 Alternativa D
Universidade do Estado de Minas Gerais 2007
(UEMG 2007) Uma secretária possui 6 camisas, 4 saias e 3 pares de sapatos. O número de maneiras distintas com que a secretária poderá se arrumar usando 1 camisa, 1 saia e 1 par de sapatos corresponde a
A) 13
B) 126
C) 72
D) 54
Resposta: 6 × 4 × 3 = 72 Alternativa C
Exercício 7
No cardápio de um restaurante estão listados 3 possibilidades de entrada, 5 de prato principal, 3 bebidas e 4 sobremesas. De quantas maneiras podemos montar uma refeição nesse restaurante, com entrada, prato principal, bebida e sobremesa?
Resposta: 3 × 5 × 3 × 4 = 180
Universidade do Estado de Minas Gerais 2016
(UEMG 2016) “Genius era um brinquedo muito popular na década de 1980 (…). O brinquedo buscava estimular a memorização de cores e sons. Com formato semelhante a um OVNI, possuía 4 botões de cores distintas que emitiam sons harmônicos e se iluminavam em sequência. Cabia aos jogadores repetir o processo sem errar”.
Origem: Wikipédia, a enciclopédia livre. (Adaptado).

Considerando uma fase do jogo em que 3 luzes irão acender de forma aleatória e em sequência, podendo cada cor acender mais de uma vez.
O número máximo de formas que essa sequência de 3 luzes poderá acender é:
A) 12.
B) 24.
C) 36.
D) 64.
Resposta: 4 × 4 × 4 = 64
Alternativa D
Universidade Estadual de Goiás 2014
(UEG 2014) Na primeira fase da Copa do Mundo da FIFA de futebol no Brasil, cada time faz 3 jogos. Sabendo-se que os resultados para cada jogo são: vitória, empate ou derrota, o número de maneiras possíveis para os resultados dessa primeira fase para um time que disputa essa Copa é
a) 3
b) 9
c) 27
d) 81
Resposta: 3 × 3 × 3 = 27
Alternativa C
Universidade Federal do Espírito Santo 1996
(UFES-1996) Um “Shopping Center” possui 4 portas de entrada para o andar térreo, 5 escadas rolantes ligando o térreo ao primeiro pavimento e 3 elevadores que conduzem do primeiro para o segundo pavimento.
De quantas maneiras diferentes uma pessoa, partindo de fora do “Shopping Center” pode atingir o segundo pavimento usando os acessos mencionados?
a) 12
b) 17
c) 19
d) 23
e) 60
Resposta: 4 × 5 × 3 = 60
Alternativa E
Unifor-CE Uma sorveteria tem em seu cardápio: 16 sabores de sorvete, 3 tipos de farofa e 6 tipos de cobertura. Zilda pretende tomar apenas uma bola de sorvete, com uma única cobertura e um único tipo de farofa. Quantas são suas opções de escolha?
a) 144
b) 288
c) 324
d) 576
e) 648
Exercício 8
Uma cantina permite que você monte o seu próprio combo. No combo vem um sanduíche, um pacote de batatas, uma bebida e uma sobremesa. Na cantina eles têm 4 opções de sanduíche, 3 tamanhos de pacotes de batata, 5 opções de bebida e 6 opções de sobremesa. De quantas maneiras diferentes você pode montar o seu combo?
Resposta: 4 × 3 × 5 × 6 = 360
Exercício 9
Joãozinho quer se vestir com calça, camiseta, sapato e boné. No seu armário, Joãozinho tem 4 calças, 5 camisetas, 2 pares de sapato e 3 bonés. De quantas maneiras diferentes Joãozinho pode se vestir?
Resposta: 4 × 5 × 2 × 3 = 120
Universidade Estadual de Londrina 1996
(UEL-1996) Para responder a certo questionário, preenche-se o cartão apresentado a seguir, colocando-se um “x” em uma só resposta para cada questão.

De quantas maneiras distintas pode-se responder a esse questionário?
a) 3 125
b) 120
c) 32
d) 25
e) 15
Resposta: 2 × 2 × 2 × 2 × 2 = 32
Alternativa C
(UFRN 2010) A figura ao lado mostra um quadro com sete lâmpadas fluorescentes, as quais podem estar acesas ou apagadas, independentemente umas das outras. Cada uma das situações possíveis corresponde a um sinal de um código.

Nesse caso, o número total de sinais possíveis é
A) 21
B) 42
C) 128
D) 256
ENEM 2019 PPL
(ENEM 2019 PPL) Uma pessoa comprou um aparelho sem fio para transmitir músicas a partir do seu computador para o rádio de seu quarto. Esse aparelho possui quatro chaves seletoras e cada uma pode estar na posição 0 ou 1.Cada escolha das posições dessas chaves corresponde a uma frequência diferente de transmissão.
A quantidade de frequências diferentes que esse aparelho pode transmitir é determinada por
A 6.
B 8.
C 12.
D 16.
E 24.
Dica 1:
Dica 2:
Conclusão da Dica 2:
Resposta: 2 × 2 × 2 × 2 = 16
Alternativa D
ENEM 2007
(ENEM 2007) Estima-se que haja, no Acre, 209 espécies de mamíferos, distribuídas conforme a tabela abaixo.
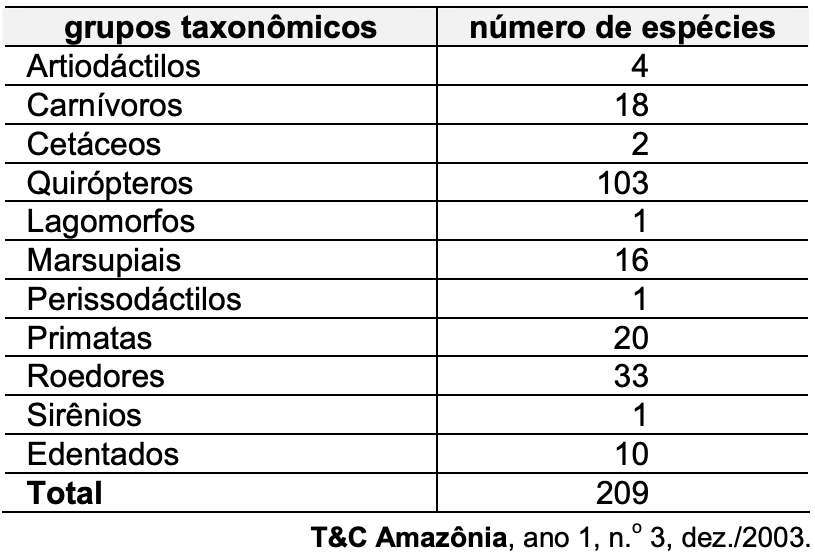
Deseja-se realizar um estudo comparativo entre três dessas espécies de mamíferos — uma do grupo Cetáceos, outra do grupo Primatas e a terceira do grupo Roedores. O número de conjuntos distintos que podem ser formados com essas espécies para esse estudo é igual a
A 1.320.
B 2.090.
C 5.845.
D 6.600.
E 7.245.
Resposta: 2 × 20 × 33 = 1320
Alternativa A
(ENEM 2012) O diretor de uma escola convidou os 280 alunos de terceiro ano a participarem de uma brincadeira. Suponha que existem 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa.
O objetivo da brincadeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido.
Todos os alunos decidiram participar. A cada vez um aluno é sorteado e dá a sua resposta. As respostas devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é declarado vencedor e a brincadeira é encerrada.
O diretor sabe que algum aluno acertará a resposta porque há
A 10 alunos a mais do que possíveis respostas distintas.
B 20 alunos a mais do que possíveis respostas distintas.
C 119 alunos a mais do que possíveis respostas distintas.
D 260 alunos a mais do que possíveis respostas distintas.
E 270 alunos a mais do que possíveis respostas distintas.
Universidade do Estado da Bahia – 1998
(Uneb-1998) Uma senhora idosa foi retirar dinheiro em um caixa automático, mas se esqueceu da senha. Lembrava que não havia o algarismo 0, que o primeiro algarismo era 8, o segundo era par, o terceiro era menor que 5 e o quarto e último era ímpar. Qual o maior
número de tentativas que ela pode fazer, no intuito de acertar a senha?
a) 13
b) 60
c) 75
d) 78
e) 80
Resposta: 1 × 4 × 4 × 5 = 80
Alternativa E
Que nota você daria para este tutorial?
Você completou o Passo 3 do programa: Probabilidades e Análise Combinatória – Passo a Passo do básico ao avançado.


