(ENEM 2020) O Estatuto do Idoso, no Brasil, prevê certos direitos às pessoas com idade avançada, concedendo a estas, entre outros benefícios, a restituição de imposto de renda antes dos demais contribuintes. A tabela informa os nomes e as idades de 12 idosos que aguardam suas restituições de imposto de renda. Considere que, entre os idosos, a restituição seja concedida em ordem decrescente de idade e que, em subgrupos de pessoas com a mesma idade, a ordem seja decidida por sorteio.
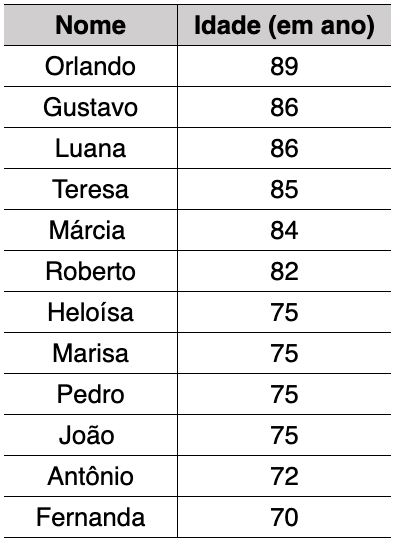
Nessas condições, a probabilidade de João ser a sétima pessoa do grupo a receber sua restituição é igual a:
A) 1/12
B) 7/12
C) 1/8
D) 5/6
E) 1/4
Exercício ENEM 2013
(ENEM 2013 2a aplicação) Uma empresa aérea lança uma promoção de final de semana para um voo comercial. Por esse motivo, o cliente não pode fazer reservas e as poltronas serão sorteadas aleatoriamente. A figura mostra a posição dos assentos no avião:
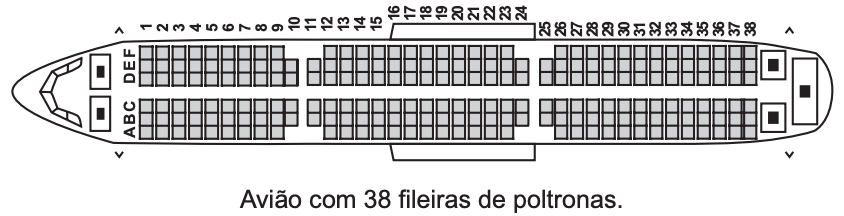
Por ter pavor de sentar entre duas pessoas, um passageiro decide que só viajará se a chance de pegar uma dessas poltronas for inferior a 30%.
Avaliando a figura, o passageiro desiste da viagem, porque a chance de ele ser sorteado com uma poltrona entre duas pessoas é mais aproximada de
a) 31%
b) 33%
c) 35%
d) 68%
e) 69%
Dica 1:
Dica 2:
Dica 3:
Dica 4:
Dica 4 Resolução:
Resposta: Alternativa A
(ENEM 2005) As 23 ex-alunas de uma turma que completou o Ensino Médio há 10 anos se encontraram em uma reunião comemorativa. Várias delas haviam se casado e tido filhos. A distribuição das mulheres, de acordo com a quantidade de filhos, é mostrada no gráfico abaixo.
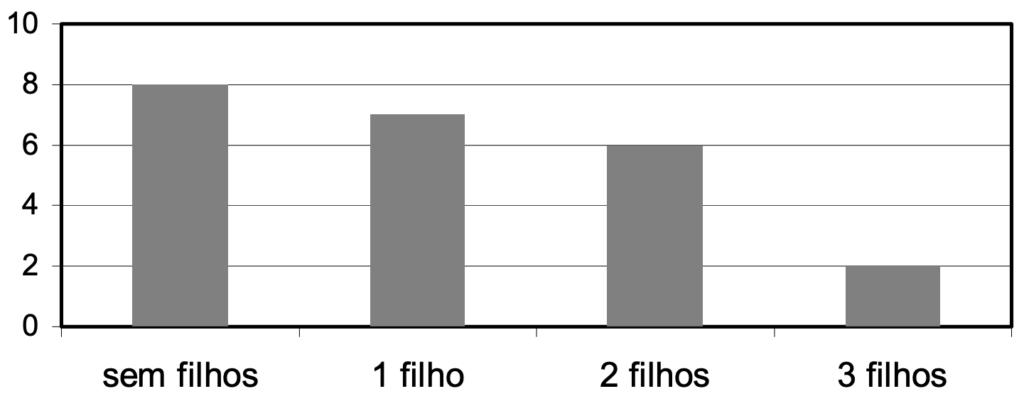
Um prêmio foi sorteado entre todos os filhos dessas ex-alunas. A probabilidade de que a criança premiada tenha sido um(a) filho(a) único(a) é
A) 1/3.
B) 1/4.
C) 7/15.
D) 7/23.
E) 7/25.
Resposta: Alternativa E
(ENEM 2006) A tabela ao lado indica a posição relativa de quatro times de futebol na classificação geral de um torneio, em dois anos consecutivos. O símbolo ● significa que o time indicado na linha ficou, no ano de 2004, à frente do indicado na coluna. O símbolo * significa que o time indicado na linha ficou, no ano de 2005, à frente do indicado na coluna.

A probabilidade de que um desses quatro times, escolhido ao acaso, tenha obtido a mesma classificação no torneio, em 2004 e 2005, é igual a
A 0,00.
B 0,25.
C 0,50.
D 0,75.
E 1,00.
Resposta: Alternativa A
(FATEC) Numa aula inaugural para alunos ingressantes do turno da manhã havia 72 alunos de Edifícios, 72 de Processos de Produção e 36 de Processamento de Dados. Desses alunos, a porcentagem de mulheres em cada uma dessas modalidades é 50% em Edifícios e em Processamento de Dado, 25% em Processo de Produção.
Sorteando-se um desses alunos, a probabilidade de o mesmo ser mulher e ter ingressado no curso de Processos de Produção é
a) 1/25
b) 2/25
c) 1/10
d) 1/5
e) 2/5
Resposta: Alternativa C
(FATEC) Numa eleição para prefeito de uma certa cidade, concorreram somente os candidatos A e B. Em uma seção eleitoral votaram 250 eleitores. Do número total de votos dessa seção, 42% foram para o candidato A, 34% para o candidato B, 18% foram anulados e os restantes estavam em branco. Tirando-se, ao acaso, um voto dessa urna, a probabilidade de que seja um voto em branco é:
a) 1/100
b) 3/50
c) 1/50
d) 1/25
e) 3/20
Resposta: Alternativa E
(ENEM 2019 PPL) Uma locadora possui disponíveis 120 veículos da categoria que um cliente pretende locar. Desses, 20% são da cor branca, 40% são da cor cinza, 16 veículos são da cor vermelha e o restante, de outras cores.
O cliente não gosta da cor vermelha e ficaria contente com qualquer outra cor, mas o sistema de controle disponibiliza os veículos sem levar em conta a escolha da cor pelo cliente.
Disponibilizando aleatoriamente, qual é a probabilidade de o cliente ficar contente com a cor do veículo?
A) \(\frac{16}{120}\)
B) \(\frac{32}{120}\)
C) \(\frac{72}{120}\)
D) \(\frac{101}{120}\)
E) \(\frac{104}{120}\)
Exercício ENEM 2011
(ENEM 2011)O gráfico mostra a velocidade de conexão à internet utilizada em domicílios no Brasil. Esses dados são resultado da mais recente pesquisa, de 2009, realizada pelo Comitê Gestor de Internet (CGI).
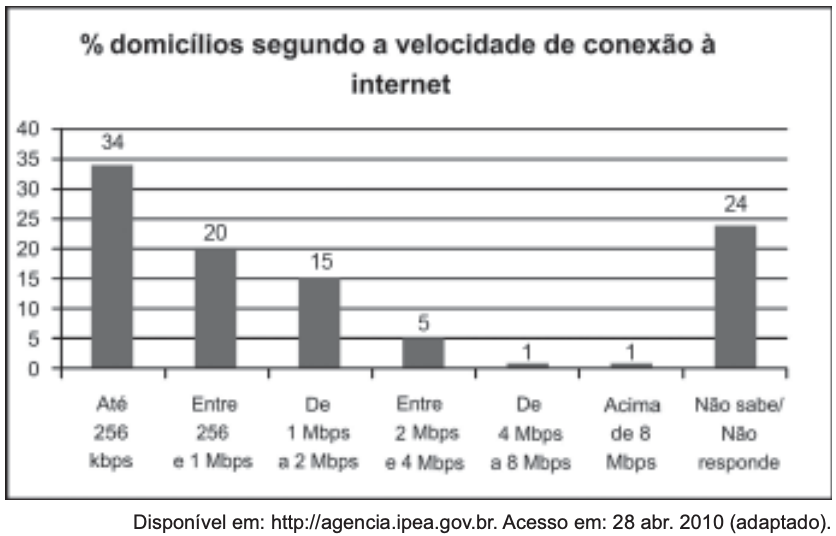
Escolhendo-se aleatoriamente, um domicílio pesquisado, qual a chance de haver banda larga de conexão de pelo menos 1Mbps neste domicílio?
a) 0,45
b) 0,42
c) 0,30
d) 0,22
e) 0,15
Exercício ENEM 2009
(ENEM 2009) A população mundial está ficando mais velha, os índices de natalidade diminuíram e a expectativa de vida aumentou. No gráfico seguinte, são apresentados dados obtidos por pesquisa realizada pela Organização das Nações Unidas (ONU), a respeito da quantidade de pessoas com 60 anos ou mais em todo o mundo. Os números da coluna da direita representam as faixas percentuais. Por exemplo, em 1950 havia 95 milhões de pessoas com 60 anos ou mais nos países desenvolvidos, número entre 10% e 15% da população total nos países desenvolvidos.
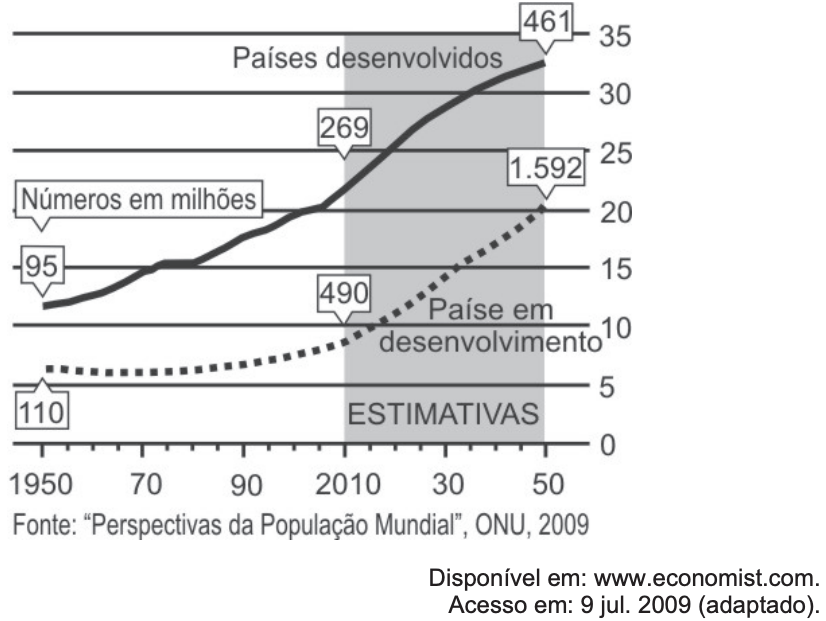
Em 2050, a probabilidade de se escolher, aleatoriamente, uma pessoa com 60 anos ou mais de idade, na população dos países desenvolvidos, será um número mais próximo de
a) \(\frac{1}{2}\)
b) \(\frac{7}{20}\)
c) \(\frac{8}{25}\)
d) \(\frac{1}{5}\)
e) \(\frac{3}{25}\)
(ENEM 2020 Digital) Um apostador deve escolher uma entre cinco moedas ao acaso e lançá-la sobre uma mesa, tentando acertar qual resultado (cara ou coroa) sairá na face superior da moeda.
Suponha que as cinco moedas que ele pode escolher sejam diferentes:
• duas delas têm “cara” nas duas faces;
• uma delas tem “coroa” nas duas faces;
• duas delas são normais (cara em uma face e coroa na outra).
Nesse jogo, qual é a probabilidade de o apostador obter uma face “cara” no lado superior da
moeda lançada por ele?
A 1/8
B 2/5
C 3/5
D 3/4
E 4/5
(ENEM 2012) Em um jogo há duas urnas com 10 bolas de mesmo tamanho em cada urna. A tabela a seguir indica as quantidades de bolas de cada cor em cada urna.
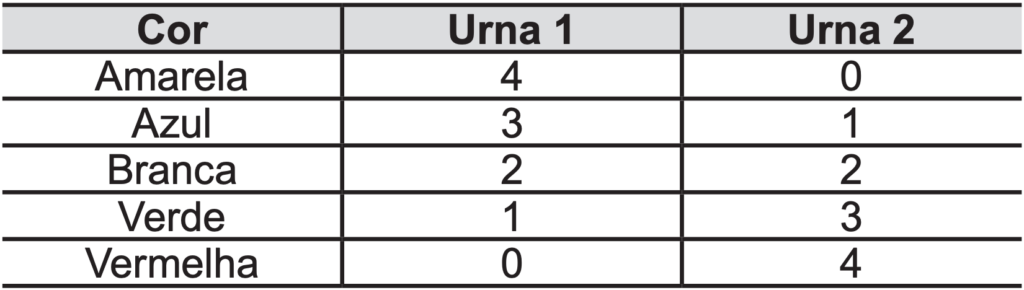
Uma jogada consiste em:
1º) o jogador apresenta um palpite sobre a cor da bola que será retirada por ele da urna 2;
2º) ele retira, aleatoriamente, uma bola da urna 1 e a coloca na urna 2, misturando-a com as que lá estão;
3º) em seguida ele retira, também aleatoriamente, uma bola da urna 2;
4º) se a cor da última bola retirada for a mesma do palpite inicial, ele ganha o jogo.
Qual cor deve ser escolhida pelo jogador para que ele tenha a maior probabilidade de ganhar?
A Azul.
B Amarela.
C Branca.
D Verde.
E Vermelha.
(UFSCAR – Candidatos Indígenas 2016) Em um cesto, há 32 frutas, sendo que \(\frac{1}{16}\) delas estão estragadas e, das demais frutas, 6 estão verdes e as outras estão maduras. Retirando-se uma fruta ao acaso desse cesto, a fração que representa a chance de ela estar madura entre as 32 frutas do cesto é
(A) \(\frac{1}{4}\)
(B) \(\frac{2}{5}\)
(C) \(\frac{1}{2}\)
(D) \(\frac{2}{3}\)
(E) \(\frac{3}{4}\)
(UFSCAR – Candidatos Indígenas 2017) Em um pacote, há 20 balas de chocolate e 16 balas de leite. Jardel comeu \(\frac{1}{5}\) das balas de chocolate, e seu primo comeu \(\frac{1}{4}\) das balas de leite. Todas as balas restantes foram colocadas em um pote. Se o irmão de Jardel retirar uma bala desse pote, a chance de a bala ser de chocolate é de
(A) 5 em 9.
(B) 4 em 9.
(C) 4 em 7.
(D) 3 em 7.
(E) 3 em 8.
(FATEC 2011) Em uma urna há dezoito bolas amarelas, algumas bolas vermelhas e outras bolas brancas, todas indistinguíveis pelo tato, e sabe-se que a quantidade de bolas brancas é igual ao dobro das vermelhas.
Se a probabilidade de se retirar, ao acaso, uma bola amarela da urna é \(\frac{2}{5}\), a quantidade de bolas vermelhas que há na urna é
(A) 8.
(B) 9.
(C) 12.
(D) 18.
(E) 24.
(FGV 2014) Em uma urna há 72 bolas idênticas mas com cores diferentes. Há bolas brancas, vermelhas e pretas. Ao sortearmos uma bola da urna, a probabilidade de ela ser branca é 1/4 e a probabilidade de ela ser vermelha é 1/ 3 .
A diferença entre o número de bolas pretas e o número de bolas brancas na urna é
A) 12
B) 10
C) 8
D) 6
E) 4
(ENEM 2018) O gerente do setor de recursos humanos de uma empresa está organizando uma avaliação em que uma das etapas é um jogo de perguntas e respostas. Para essa etapa, ele classificou as perguntas, pelo nível de dificuldade, em fácil, médio e difícil, e escreveu cada pergunta em cartões para colocação em uma urna.
Contudo, após depositar vinte perguntas de diferentes níveis na urna, ele observou que 25% delas eram de nível fácil. Querendo que as perguntas de nível fácil sejam a maioria, o gerente decidiu acrescentar mais perguntas de nível fácil à urna, de modo que a probabilidade de o primeiro participante retirar, aleatoriamente, uma pergunta de nível fácil seja de 75%.
Com essas informações, a quantidade de perguntas de nível fácil que o gerente deve acrescentar à urna é igual a:
A) 10.
B) 15.
C) 35.
D) 40.
E) 45.
(ENEM 2017) A figura ilustra uma partida de Campo Minado, o jogo presente em praticamente todo computador pessoal. Quatro quadrados em um tabuleiro 16 u 16 foram abertos, e os números em suas faces indicam quantos dos seus 8 vizinhos contêm minas (a serem evitadas). O número 40 no canto inferior direito é o número total de minas no tabuleiro, cujas posições foram escolhidas ao acaso, de forma uniforme, antes de se abrir qualquer quadrado.

Em sua próxima jogada, o jogador deve escolher dentre os quadrados marcados com as letras P, Q, R, S e T um para abrir, sendo que deve escolher aquele com a menor probabilidade de conter uma mina.
O jogador deverá abrir o quadrado marcado com a letra
A P.
B Q.
C R.
D S.
E T.
(ENEM 2009) Dados do Instituto de Pesquisas Econômicas Aplicadas (IPEA) revelaram que no biênio 2004/2005, nas rodovias federais, os atropelamentos com morte ocuparam o segundo lugar no ranking de mortalidade por acidente. A cada 34 atropelamentos, ocorreram 10 mortes. Cerca de 4 mil atropelamentos/ano, um a cada duas horas, aproximadamente.
Disponível em: http://www.ipea.gov.br. Acesso em: 6 jan. 2009.
De acordo com os dados, se for escolhido aleatoriamente para investigação mais detalhada um dos atropelamentos ocorridos no biênio 2004/2005, a probabilidade de ter sido um atropelamento sem morte é
A) \(\frac{2}{17}\)
B) \(\frac{5}{17}\)
C) \(\frac{2}{5}\)
D) \(\frac{3}{5}\)
E) \(\frac{12}{17}\)
Exercício ENEM 2012
(ENEM 2012 2a aplicação) Uma coleta de dados em mais de 5 mil sites da internet apresentou os conteúdos de interesse de cada faixa etária. Na tabela a seguir estão os dados obtidos para a faixa etária de 0 a 17 anos.
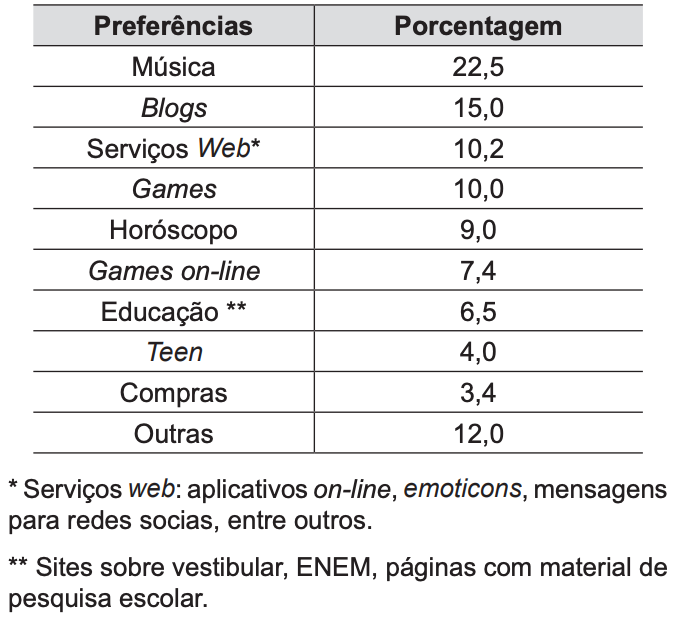
Considere que esses dados refletem os interesses dos brasileiros desta faixa etária.
Disponível em: www.navegg.com. Acesso em: 12 nov. 2011(adaptado)
Selecionando, ao acaso, uma pessoa desta faixa etária, a probabilidade de que ela não tenha preferência por horóscopo é
a) 0,09
b) 0,10
c) 0,11
d) 0,79
e) 0,91
(ENEM 2020) Suponha que uma equipe de corrida de automóveis disponha de cinco tipos de pneu (I, II, III, IV, V) em que o fator de eficiência climática EC (índice que fornece o comportamento do pneu em uso, dependendo do clima) é apresentado:
- EC do pneu I: com chuva 6, sem chuva 3;
- EC do pneu II: com chuva 7, sem chuva -4;
- EC do pneu III: com chuva -2, sem chuva 10;
- EC do pneu IV: com chuva 2, sem chuva 8;
- EC do pneu V: com chuva -6, sem chuva 7;
O coeficiente de rendimento climático (CRC) de um pneu é calculado com a soma dos produtos dos fatores de EC, com ou sem chuva, pelas correspondentes probabilidades de se ter tais condições climáticas: ele é utilizado para determinar qual pneu deve ser selecionado para uma dada corrida, escolhendo-se o pneu que apresentar o maior CRC naquele dia. No dia de certa corrida, a probabilidade de chover era de 70% e o chefe da equipe calculou o CRC de cada um dos cinco tipos de pneu.
O pneu escolhido foi:
A) I
B) II
C) III
D) IV
E) V

