Geometria – Ângulos

(ENEM 2017) Raios de luz solar estão atingindo a superfície de um lago formando um ângulo x com a sua superfície, conforme indica a figura.

Em determinadas condições, pode-se supor que a intensidade luminosa desses raios, na superfície do lago, seja dada aproximadamente por I(x)=k.sen(x) sendo k uma constante, e supondo-se que x está entre 0^o e 90^o.

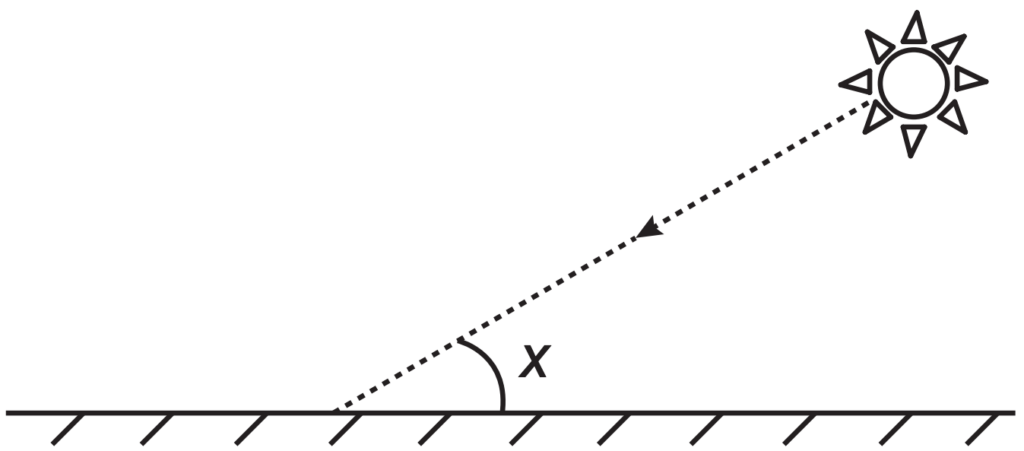
Quando x = 30^o, a intensidade luminosa se reduz a qual percentual de seu valor máximo?

A) 33%
B) 50%
C) 57%
D) 70%
E) 86%

(ENEM 2011) O polígono que dá forma a essa calçada é invariante por rotações, em torno de seu centro, de
A 45°.
B 60°.
C 90°.
D 120°.
E 180°.

Exercício

A figura abaixo representa um triângulo retângulo com ângulos de \(30^o\), \(60^o\) e \(90^o\). O lado AB mede \(2\sqrt{3}\). Calcule a medida dos lados BC e AC

Exercício

A altura de um triângulo equilátero mede \(\frac{\sqrt{3}}{2}\). Quanto mede o lado do triângulo?

(ENEM 2012 PPL) Durante seu treinamento, um atleta percorre metade de uma pista circular de raio R, conforme figura a seguir. A sua largada foi dada na posição representada pela letra L, a chegada está representada pela letra C e a letra A representa o atleta. O segmento LC é um diâmetro da circunferência e o centro da circunferência está representado pela letra F.

Sabemos que, em qualquer posição que o atleta esteja na pista, os segmentos LA e AC são perpendiculares. Seja θ o ângulo que o segmento AF faz com segmento FC.

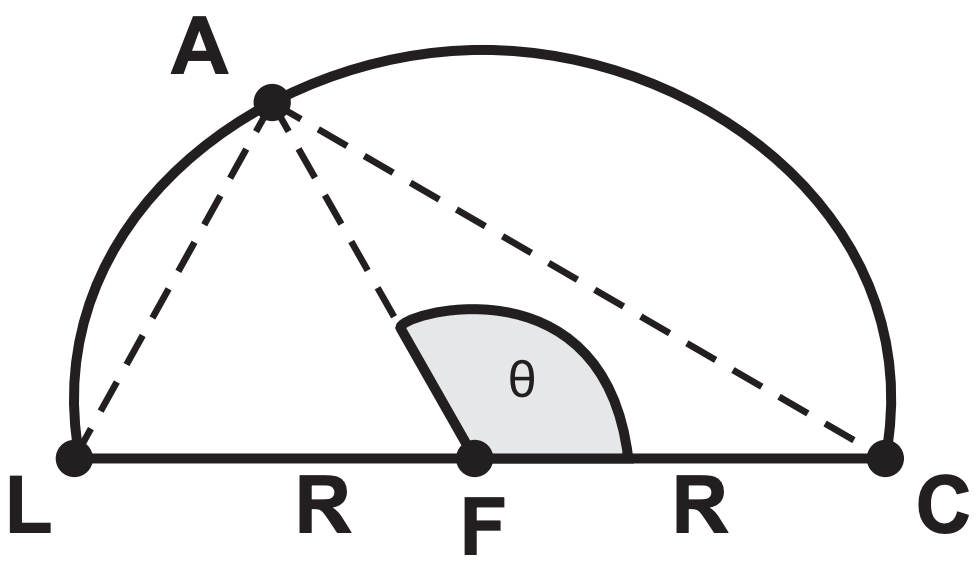
Quantos graus mede o ângulo θ quando o segmento AC medir R durante a corrida?

A 15 graus
B 30 graus
C 60 graus
D 90 graus
E 120 graus

Resposta: Alternativa C

(FAMERP 2016) No caminho de ida de sua casa (C) para a escola (E), Laura passa pela farmácia (F), pela padaria (P), e depois segue para a escola, como indica a figura 1.

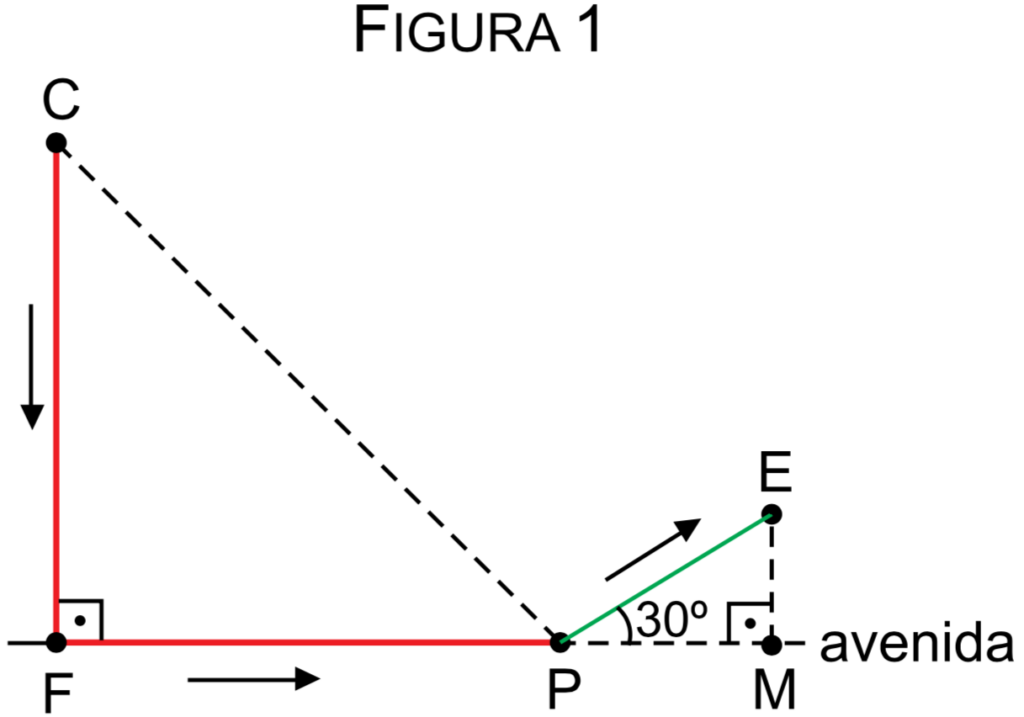
Na volta da escola para casa, Laura passa pelo mercado (M), pela padaria (P), e depois segue para casa (C), como indica a figura 2.

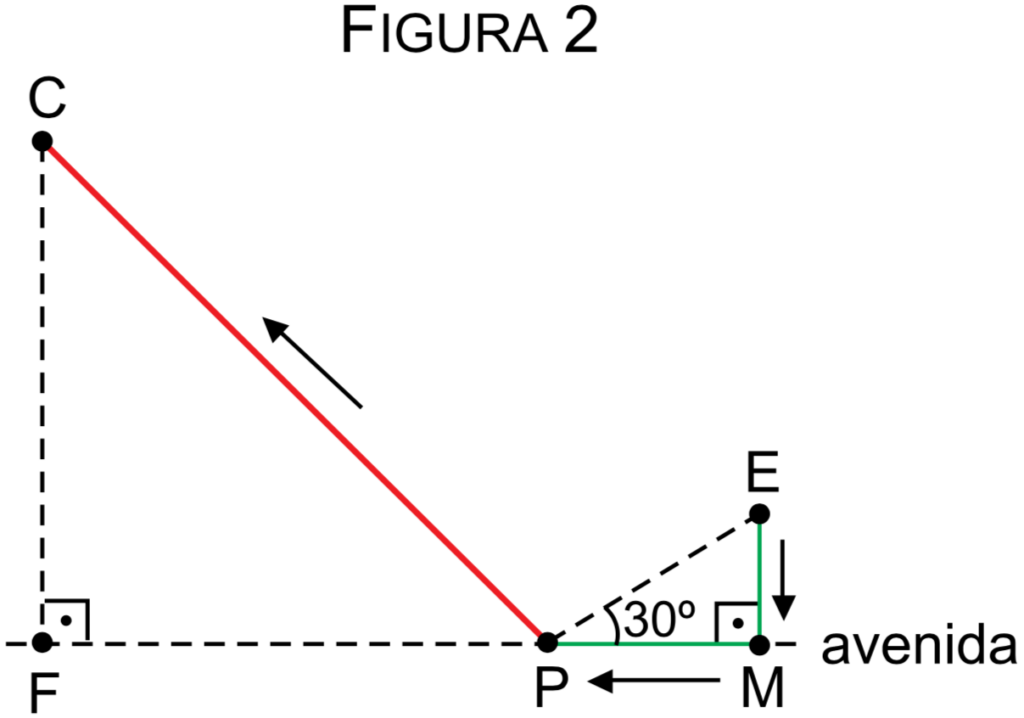
Os caminhos de ida e de volta são formados por segmentos de retas, sendo que a farmácia, a padaria e o mercado estão em uma mesma avenida reta e plana. Considerando CF = FP = 4 km, PE = 2 km, \(\sqrt{2}=1,4\) e \(\sqrt{3}=1,7\), o caminho de Laura de casa à escola na ida superou o de volta em

A) 1,7 km.
B) 2,3 km.
C) 1,2 km.
D) 2,0 km.
E) 0,9 km.

(FAMEMA 2019) A figura mostra o triângulo retângulo ABC, de hipotenusa AB = 10 cm, com o ângulo \(A\hat{B}C = 30^o\) e o ponto D sobre o lado \(\overline{BC}\).

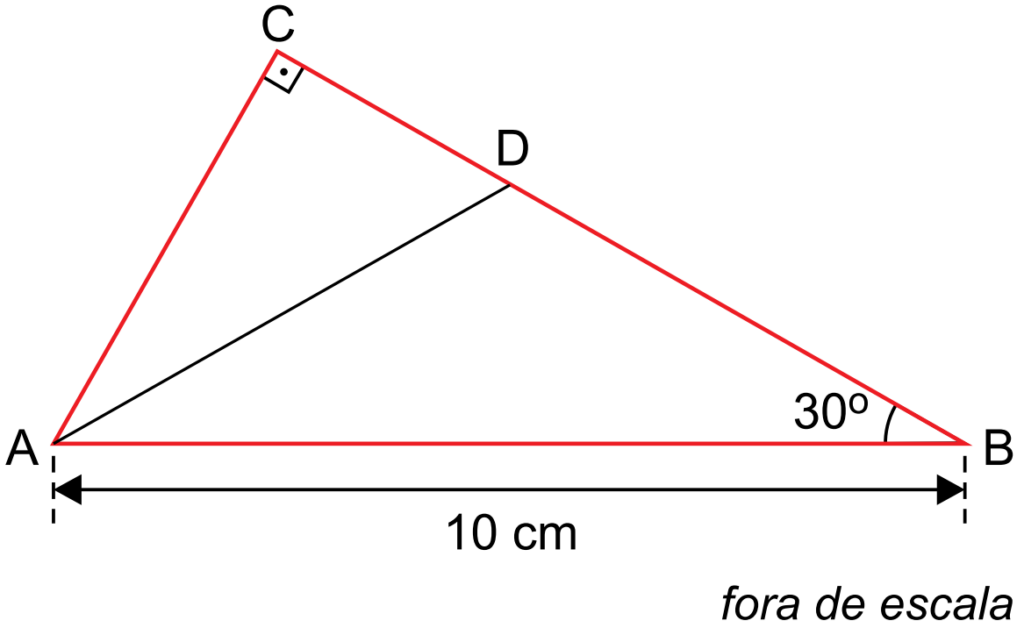
Sabendo que \(\overline{AD}\) é bissetriz do ângulo BÂC, o valor da razão \(\frac{\overline{BD}}{\overline{DC}}\) é

A) 3

B) \(\frac{1}{2}\)

C) \(\frac{1}{3}\)

D) 1

E) 2

Resposta: Alternativa E

(UFRN 2011) A Figura abaixo representa uma torre de altura H equilibrada por dois cabos de comprimentos L₁ e L₂, fixados nos pontos C e D, respectivamente.

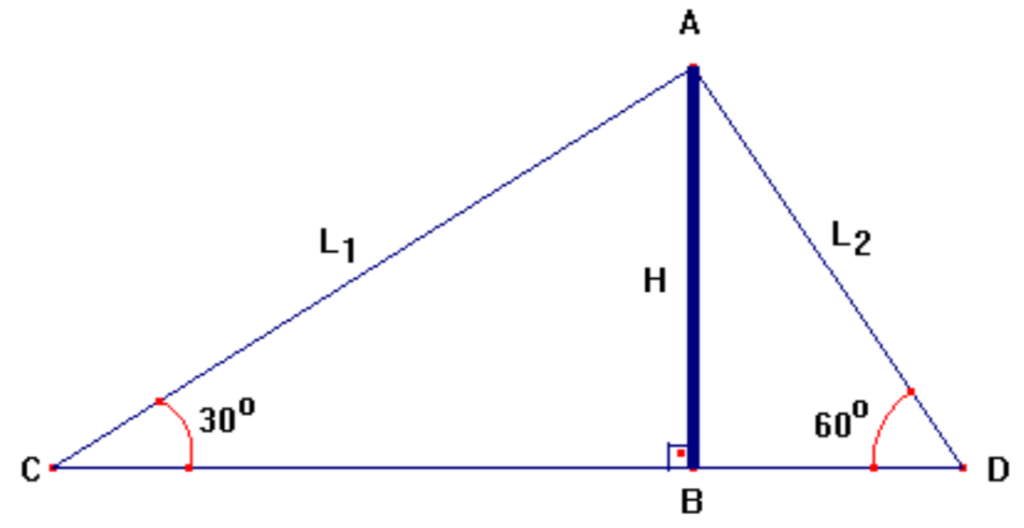
Entre os pontos B e C passa um rio, dificultando a medição das distâncias entre esses pontos. Apenas com as medidas dos ângulos C e D e a distância entre B e D, um engenheiro calculou a quantidade de cabo (L₁+ L₂) que usou para fixar a torre.

O valor encontrado, usando \(\sqrt{3}=1,73\) e BD = 10m, é

A) 54,6m. B) 44,8m. C) 62,5m. D) 48,6m.

(ENEM 2011) Para determinar a distância de um barco até a praia, um navegante utilizou o seguinte procedimento: a partir de um ponto A, mediu o ângulo visual α fazendo mira em um ponto fixo P da praia. Mantendo o barco no mesmo sentido, ele seguiu até um ponto B de modo que fosse possível ver o mesmo ponto P da praia, no entanto sob um ângulo visual 2α. A figura ilustra essa situação:

Suponha que o navegante tenha medido o ângulo α = 30^o e, ao chegar ao ponto B, verificou que o barco havia percorrido a distância AB = 2 000 m. Com base nesses dados e mantendo a mesma trajetória, a menor distância do barco até o ponto fixo P será

A)\(1000 m\)
B)\(1000\sqrt{3} m\)
C)\(2000\frac{\sqrt{3}}{3} m\)
D)\(2000 m\)
E)\(2000\sqrt{3} m\)

Resposta: Alternativa B

(ENEM 2010) Um balão atmosférico, lançado em Bauru (343 quilômetros a Noroeste de São Paulo), na noite do último domingo, caiu nesta segunda-feira em Cuiabá Paulista, na região de Presidente Prudente, assustando agricultores da região. O artefato faz parte do programa Projeto Hibiscus, desenvolvido por Brasil, França, Argentina, Inglaterra e Itália, para a medição do comportamento da camada de ozônio, e sua descida se deu após o cumprimento do tempo previsto de medição.

Disponível em: http://www.correiodobrasil.com.br. Acesso em: 02 maio 2010.

Na data do acontecido, duas pessoas avistaram o balão.
Uma estava a 1,8 km da posição vertical do balão e o avistou sob um ângulo de 60°; a outra estava a 5,5 km da posição vertical do balão, alinhada com a primeira, e no mesmo sentido, conforme se vê na figura, e o avistou sob um ângulo de 30°.

Qual a altura aproximada em que se encontrava o balão?
A) 1,8 km
B) 1,9 km
C) 3,1 km
D) 3,7 km
E) 5,5 km

Resposta: Alternativa C

(UNIFESP 2008) Tem-se um triângulo eqüilátero em que cada lado mede 6 cm.
O raio do círculo circunscrito a esse triângulo, em centímetros, mede

A) \(\sqrt{3}\)

B) \(2\sqrt{3}\)

C) 4

D) \(3\sqrt{2}\)

E) \(3\sqrt{3}\)

(ENEM 2015) O tampo de vidro de uma mesa quebrou-se e deverá ser substituído por outro que tenha a forma de círculo. O suporte de apoio da mesa tem o formato de um prisma reto, de base em forma de triângulo equilátero com lados medindo 30 cm. Uma loja comercializa cinco tipos de tampos de vidro circulares com cortes já padronizados, cujos raios medem 18 cm, 26 cm, 30 cm, 35 cm e 60 cm. O proprietário da mesa deseja adquirir nessa loja o tampo de menor diâmetro que seja suficiente para cobrir a base superior do suporte da mesa.

Considere 1,7 como aproximação para \(\sqrt{3}\).

O tampo a ser escolhido será aquele cujo raio, em centímetros, é igual a

A) 18.
B) 26.
C) 30.
D) 35.
E) 60.

Resposta: Alternativa A

(ENEM 2013) Em um sistema de dutos, três canos iguais, de raio externo 30 cm, são soldados entre si e colocados dentro de um cano de raio maior, de medida R. Para posteriormente ter fácil manutenção, é necessário haver uma distância de 10 cm entre os canos soldados e o cano de raio maior. Essa distância é garantida por um espaçador de metal, conforme a figura:

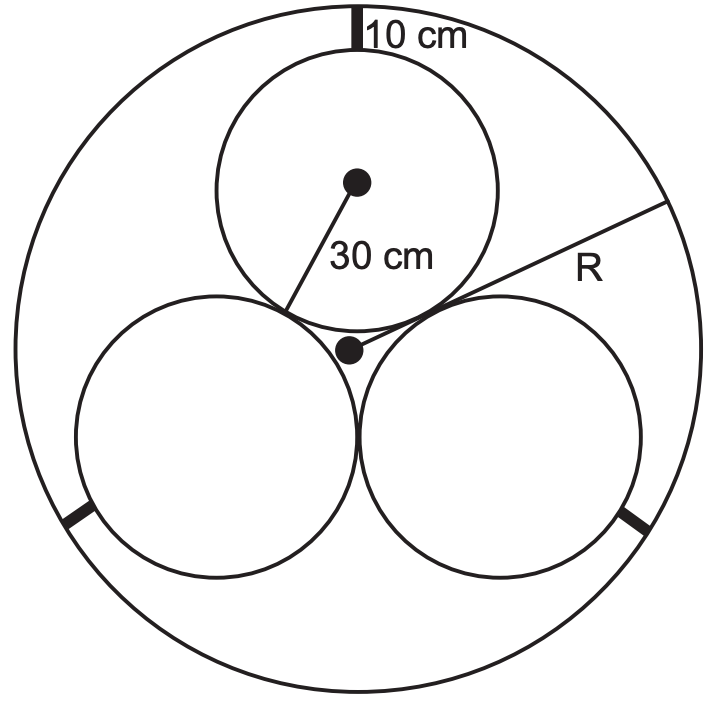
Utilize 1,7 como aproximação para \(\sqrt3\).
O valor de R, em centímetros, é igual a
A 64,0.
B 65,5.
C 74,0.
D 81,0.
E 91,0.

Resposta: Alternativa C

(UFRN 2009) Para medir a altura de uma árvore, da qual não podia aproximar-se, um ambientalista colocou, a certa distância dessa árvore, um cavalete de 1 m de altura e observou seu ponto mais alto, segundo um ângulo de 30^o. Aproximando-se mais 10 m, observou o mesmo ponto segundo um ângulo de 45^o, conforme a figura abaixo.

Com esse procedimento, o ambientalista obteve como resultado que a altura da árvore era de:

A) \(5\sqrt{3} + 15\)
B) \(5\sqrt{3} + 5\)
C) \(5\sqrt{3} + 6\)
D) \(5\sqrt{3} + 16\)

(UFPR 2021) Na figura ao lado, há uma circunferência de centro C. Se o ângulo α mede π/3 radianos, a razão entre a área do setor circular PCQ e a área do triângulo PCQ é:

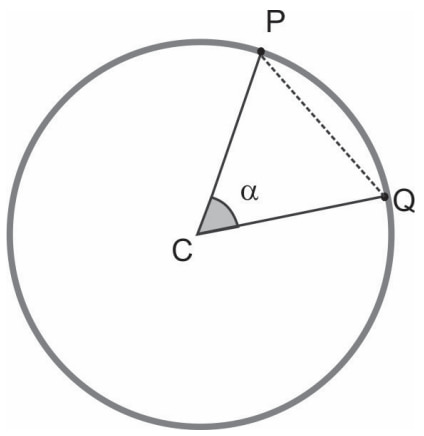
A) \(\frac{\pi \sqrt{3}}{3}\)

B) \(\frac{2\pi}{3}\)

C) \(\frac{2\pi \sqrt{3}}{9}\)

D) \(\frac{\pi \sqrt{3}}{6}\)

E) \(\frac{4\pi \sqrt{3}}{9}\)

(ENEM 2017) A manchete demonstra que o transporte de grandes cargas representa cada vez mais preocupação quando feito em vias urbanas.

Caminhão entala em viaduto no Centro

Um caminhão de grande porte entalou embaixo do viaduto no cruzamento das avenidas Borges de Medeiros e Loureiro da Silva no sentido Centro-Bairro, próximo à Ponte de Pedra, na capital. Esse veículo vinha de São Paulo para Porto Alegre e transportava três grandes tubos, conforme ilustrado na foto.

Considere que o raio externo de cada cano da imagem seja 0,60 m e que eles estejam em cima de uma carroceria cuja parte superior está a 1,30 m do solo. O desenho representa a vista traseira do empilhamento dos canos.

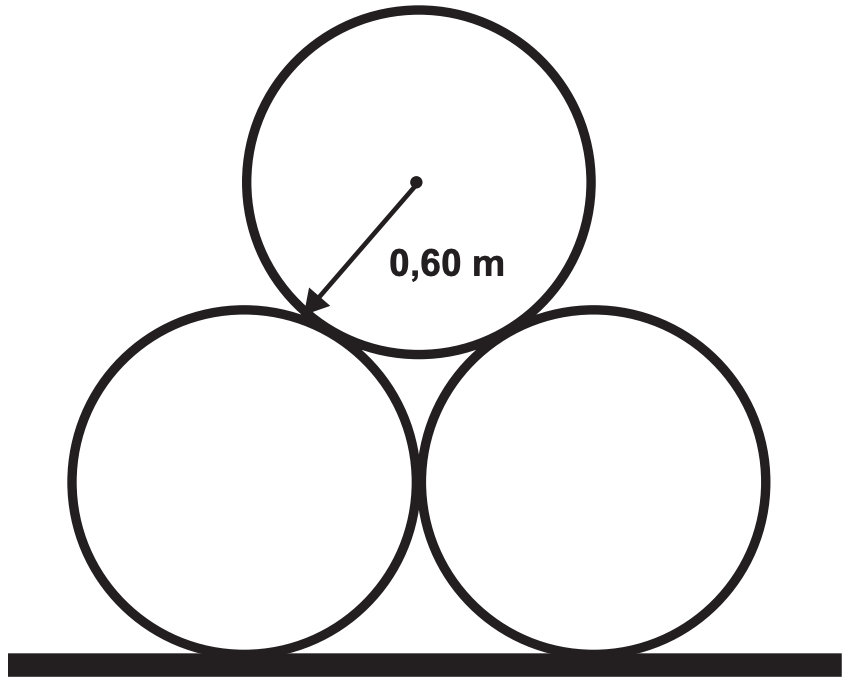
A margem de segurança recomendada para que um veículo passe sob um viaduto é que a altura total do veículo com a carga seja, no mínimo, 0,50 m menor do que a altura do vão do viaduto.

Considere 1,7 como aproximação para \(\sqrt{3}\)

Qual deveria ser a altura mínima do viaduto, em metro, para que esse caminhão pudesse passar com segurança sob seu vão?

A 2,82
B 3,52
C 3,70
D 4,02
E 4,20

(UNEMAT 2019) A medida da área do hexágono regular da figura abaixo é \(24\sqrt{3}cm^2\). As diagonais AD e BE definem dois losangos congruentes e simétricos inscritos no hexágono.

Sabendo-se que as diagonais AD e BE medem 8 cm, assinale a alternativa correta que corresponde à área ocupada pelos losangos.

A) \(16\sqrt{3}cm^2\)
B) \(8\sqrt{3}cm^2\)
C) \(\frac{16\sqrt{3}}{3}cm^2\)
D) \(18\sqrt{3}cm^2\)
E) \(6\sqrt{3}cm^2\)

(ENEM 2018 Reaplicação PPL) Um brinquedo chamado pula-pula, quando visto de cima, consiste de uma cama elástica com contorno em formato de um hexágono regular.

Se a área do círculo inscrito no hexágono é 3\(\pi\) metros quadrados, então a área do hexágono, em metro quadrado, é

A) 9
B) 6\(\sqrt{3}\)
C) 9\(\sqrt{2}\)
D) 12
E) 12\(\sqrt{3}\)