(ENEM 2020) Enquanto um ser está vivo, a quantidade de carbono 14 nele existente não se altera. Quando ele morre, essa quantidade vai diminuindo. Sabe-se que a meia-vida do carbono 14 é de 5 730 anos, ou seja, num fóssil de um organismo que morreu há 5 730 anos haverá metade do carbono 14 que existia quando ele estava vivo. Assim, cientistas e arqueólogos usam a seguinte fórmula para saber a idade de um fóssil encontrado: \( Q_t = Q_0 ∙ 2 ^{-\frac{t} {5730}} \) em que t é o tempo, medido em ano, Q(t) é a quantidade de carbono 14 medida no instante t e Q0 é a quantidade de carbono 14 no ser vivo correspondente.
Um grupo de arqueólogos, numa de suas expedições, encontrou 5 fósseis de espécies conhecidas e mediram a quantidade de carbono 14 neles existente. Na tabela temos esses valores juntamente com a quantidade de carbono 14 nas referidas espécies vivas.
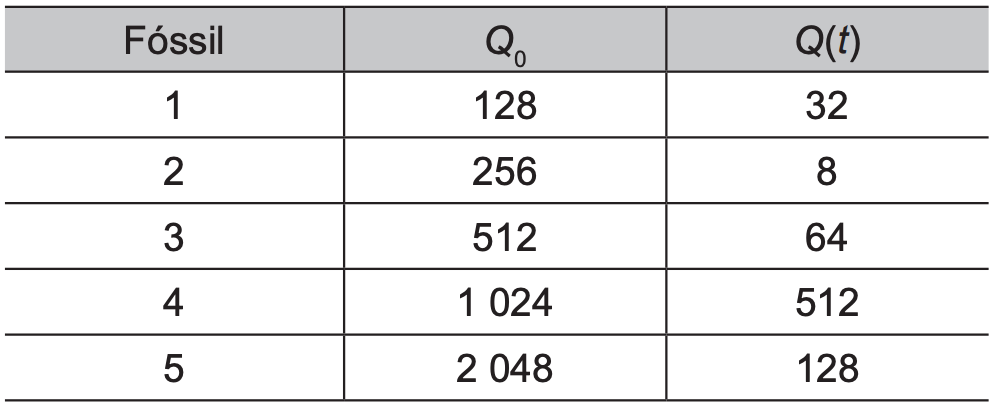
O fóssil mais antigo encontrado nessa expedição foi
A 1.
B 2.
C 3.
D 4.
E 5.
Dicas e Resolução
Dica 1
Vamos começar analisando o fóssil 1:
| Fóssil | Q0 | Q(t) |
| 1 | 128 | 32 |
Vamos substituir os valores de Q0 e Q(t) na fórmula:
\(Q_t = Q_0 ∙ 2 ^{-\frac{t} {5730}}\)
\(\iff 32 = 128∙ 2 ^{-\frac{t} {5730}}\)
Agora, podemos passar o 128 dividindo para o outro lado
\(\frac{32}{128} = 2 ^{-\frac{t} {5730}}\)
Podemos simplificar a fração \(\frac{32}{128}\), dividindo o numerador e o denominador por 2.
\(\frac{16}{64} = 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{8}{32} = 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{1}{4} = 2 ^{-\frac{t} {5730}}\)
A equação compara \(\frac{1}{4}\) com uma potência de 2.
Então, vamos escrever \(\frac{1}{4}\) na notação exponencial.
Bom, a gente sabe que \(4 = 2 \times 2 = 2^2\).
Então, \(\frac{1}{4} = 2^{-2}\).
Voltando para a equação:
\(2^{-2} = 2 ^{-\frac{t} {5730}}\)
Se as duas potências de 2 acima são iguais, então os expoentes são iguais.
\(-2 = -\frac{t}{5730}\)
\(\iff 2 = \frac{t}{5730}\)
\(\iff 2 \times 5730 = t\)
\(\iff 11460 = t \iff t = 11460\) anos
Encontramos o valor de t! O fóssil 1 possui 11460 anos.
Dica 2
Agora, repita o mesmo raciocínio para os demais fósseis.
Resolução da Dica 2
Fóssil 2
| Fóssil | Q0 | Q(t) |
| 2 | 256 | 8 |
\(Q_t = Q_0 ∙ 2 ^{-\frac{t} {5730}}\)
\(\iff 8 = 256 ∙ 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{8}{256} = 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{4}{128} = 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{2}{64} = 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{1}{32} = 2 ^{-\frac{t} {5730}}\)
A gente sabe que \(32 = 2^5\), então \(\frac{1}{32} = 2^{-5}\).
\(2^{-5} = 2 ^{-\frac{t} {5730}}\)
\(\iff -5 = -\frac{t} {5730}\)
\(\iff 5 = \frac{t} {5730}\)
\(\iff 5 \times 5730 = t\)
\(\iff 28650 = t \iff t = 28650\) anos
O fóssil 2 possui 28650 anos.
Fóssil 3
| Fóssil | Q0 | Q(t) |
| 3 | 512 | 64 |
\(Q_t = Q_0 ∙ 2 ^{-\frac{t} {5730}}\)
\(\iff 64 = 512 ∙ 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{64}{512} = 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{32}{256} = 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{16}{128} = 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{8}{64} = 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{1}{8} = 2 ^{-\frac{t} {5730}}\)
A gente sabe que \(8 = 2^3\), então \(\frac{1}{8} = 2^{-3}\).
\(2^{-3} = 2 ^{-\frac{t} {5730}}\)
\(\iff -3 = -\frac{t} {5730}\)
\(\iff 3 = \frac{t} {5730}\)
\(\iff 3 \times 5730 = t\)
\(\iff 17190 = t \iff t = 17190\) anos
O fóssil 3 possui 17190 anos.
Fóssil 4
| Fóssil | Q0 | Q(t) |
| 4 | 1024 | 512 |
\(Q_t = Q_0 ∙ 2 ^{-\frac{t} {5730}}\)
\(\iff 512 = 1024 ∙ 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{512}{1024} = 2 ^{-\frac{t} {5730}}\)
512 é metade de 1024, então \(\frac{512}{1024} = \frac{1}{2}\)
\(\iff \frac{1}{2} = 2 ^{-\frac{t} {5730}}\)
A gente sabe que \(\frac{1}{2} = 2^{-1}\).
\(2^{-1} = 2 ^{-\frac{t} {5730}}\)
\(\iff -1 = -\frac{t} {5730}\)
\(\iff 1 = \frac{t} {5730}\)
\(\iff 1 \times 5730 = t\)
\(\iff 5730 = t \iff t = 5730\) anos
O fóssil 4 possui 5730 anos.
Fóssil 5
| Fóssil | Q0 | Q(t) |
| 5 | 2048 | 128 |
\(Q_t = Q_0 ∙ 2 ^{-\frac{t} {5730}}\)
\(\iff 128 = 2048 ∙ 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{128}{2048} = 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{64}{1024} = 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{32}{512} = 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{16}{256} = 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{8}{128} = 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{4}{64} = 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{2}{32} = 2 ^{-\frac{t} {5730}}\)
\(\iff \frac{1}{16} = 2 ^{-\frac{t} {5730}}\)
A gente sabe que \(16 = 2^4\), então \(\frac{1}{16} = 2^{-4}\).
\(2^{-4} = 2 ^{-\frac{t} {5730}}\)
\(\iff -4 = -\frac{t} {5730}\)
\(\iff 4 = \frac{t} {5730}\)
\(\iff 4 \times 5730 = t\)
\(\iff 22920 = t \iff t = 22920\) anos
O fóssil 5 possui 22920 anos.
Dica 3
Qual fóssil é o mais antigo?
Resolução da Dica 3
| Fóssil | Idade |
| 1 | 11460 anos |
| 2 | 28650 anos |
| 3 | 17190 anos |
| 4 | 5730 anos |
| 5 | 22920 anos |
O fóssil 2 é o mais antigo.
Resposta
Alternativa B

