ENEM 2019 PPL – Uma pista circular delimitada por duas circunferências concêntricas foi construída

(ENEM 2019 PPL) Uma pista circular delimitada por duas circunferências concêntricas foi construída. Na circunferência interna dessa pista, de raio 0,3 km, serão colocados aparelhos de ginástica localizados nos pontos P, Q e R, conforme a figura.

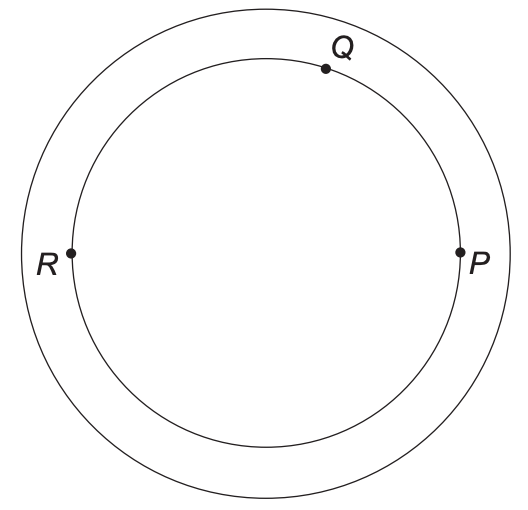
O segmento RP é um diâmetro dessa circunferência interna, e o ângulo PRQ tem medida igual a π/5 radianos.

Para uma pessoa ir do ponto P ao ponto Q andando pela circunferência interna no sentido anti-horário, ela percorrerá uma distância, em quilômetro, igual a

A 0,009π
B 0,03π
C 0,06π
D 0,12π
E 0,18π

Dicas e Resolução em vídeo

Dica 1

Dica 2

Dica 3

Dica 4

Dica 5

Dica 6

Conclusão

Resposta: Alternativa D

Dicas e Resolução por escrito

O enunciado diz que RP é um diâmetro da circunferência. Logo, RP passa pelo centro da circunferência. Então, vamos traçar o diâmetro RP, e chamar o centro da circunferência de O, como na figura abaixo.

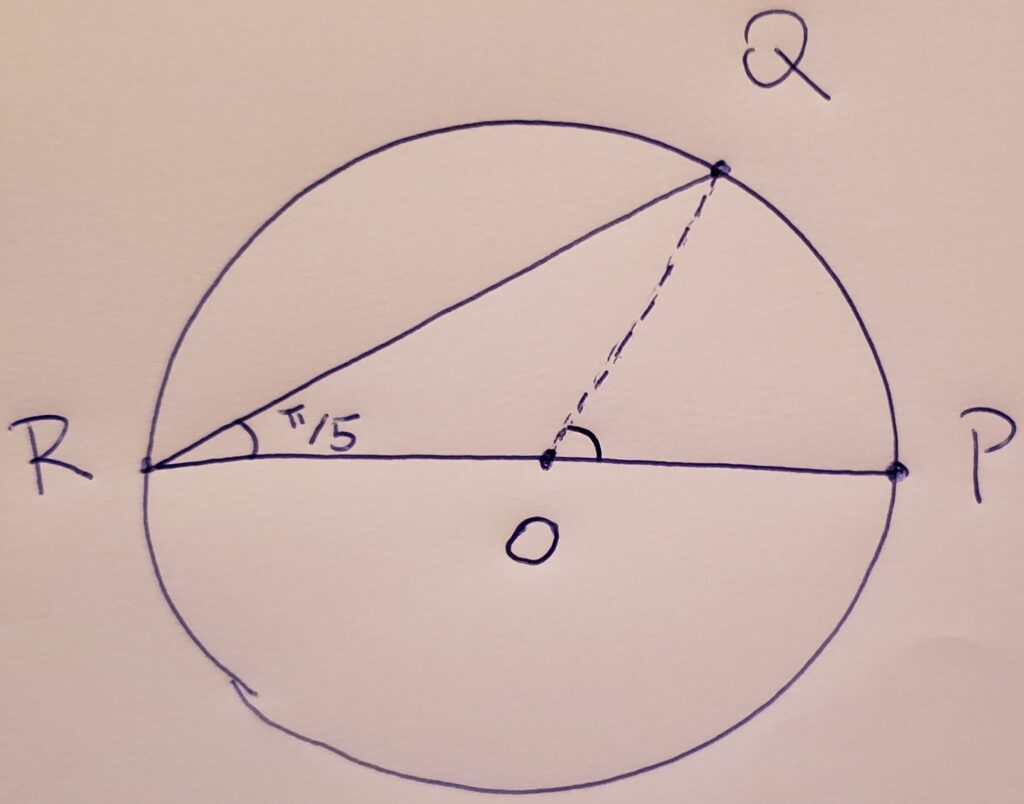
Dica 1:

O exercício pede o comprimento do arco PQ. Para fazer isso, temos antes que calcular o valor do ângulo PÔQ. Tente calcular você mesmo antes de prosseguir na resolução 🙂

Resolução da Dica 1:

Vamos olhar com calma o triângulo ROQ.

A gente pode notar que o segmento RO é um raio da circunferência. O segmento OQ também é um raio da circunferência. Logo, RO e OQ são segmentos de mesmo tamanho, iguais ao raio da circunferência.

O que a gente conclui disso? Podemos concluir que ROQ é um triângulo isósceles!

Pelo fato do triângulo ser isósceles, o ângulo ORQ é igual ao ângulo OQR. Assim, o ângulo OQR mede π/5 radianos.

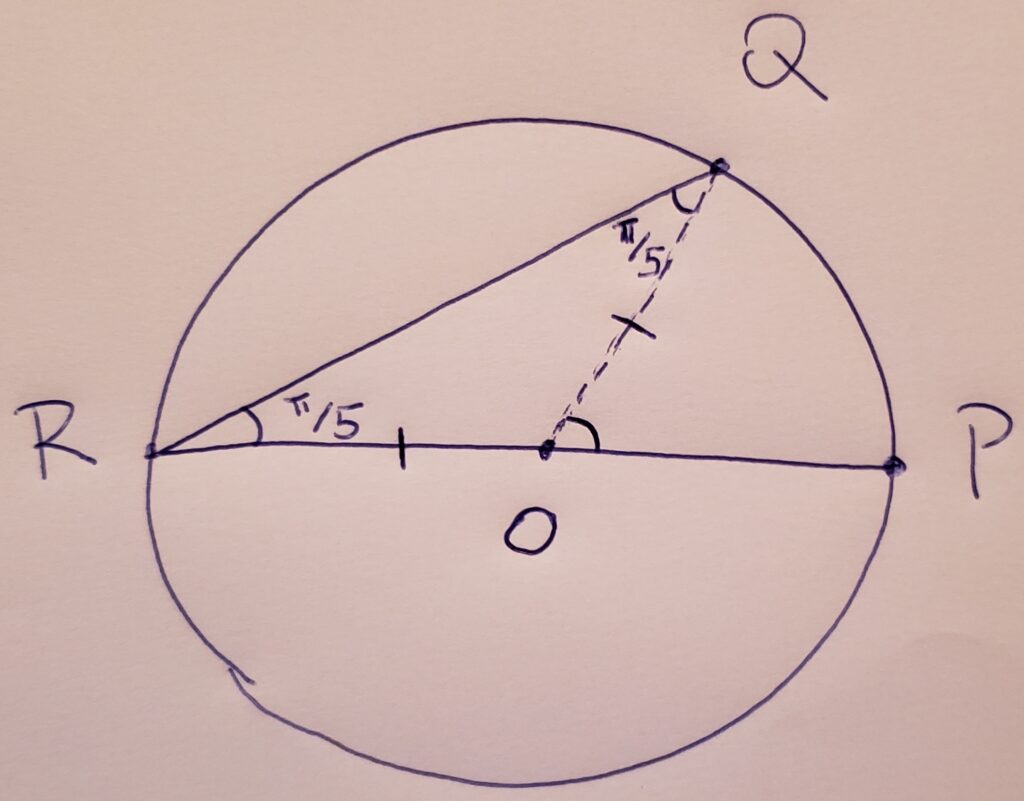
Dica 2:

No triângulo ROQ, já conhecemos dois ângulos, ambos valendo π/5 radianos. Qual é a medida do terceiro ângulo?

Resolução da Dica 2:

A gente sabe que a soma dos 3 ângulos de um triângulo é sempre 180 graus. No enunciado, os ângulos estão em radianos. Quanto vale 180 graus em radianos? Bom, 180 graus é equivalente a π radianos.

Então a soma dos três ângulos do triângulo ROQ deve valer π radianos.

Já sabemos que ORQ e OQR medem ambos π/5 radianos. Quanto vale o ângulo ROQ?

ângulo ROQ + π/5 + π/5 = π

<=> ângulo ROQ + 2π/5 = π

<=> ângulo ROQ = π – 2π/5

<=> ângulo ROQ = 5π/5 – 2π/5

<=> ângulo ROQ = 3π/5

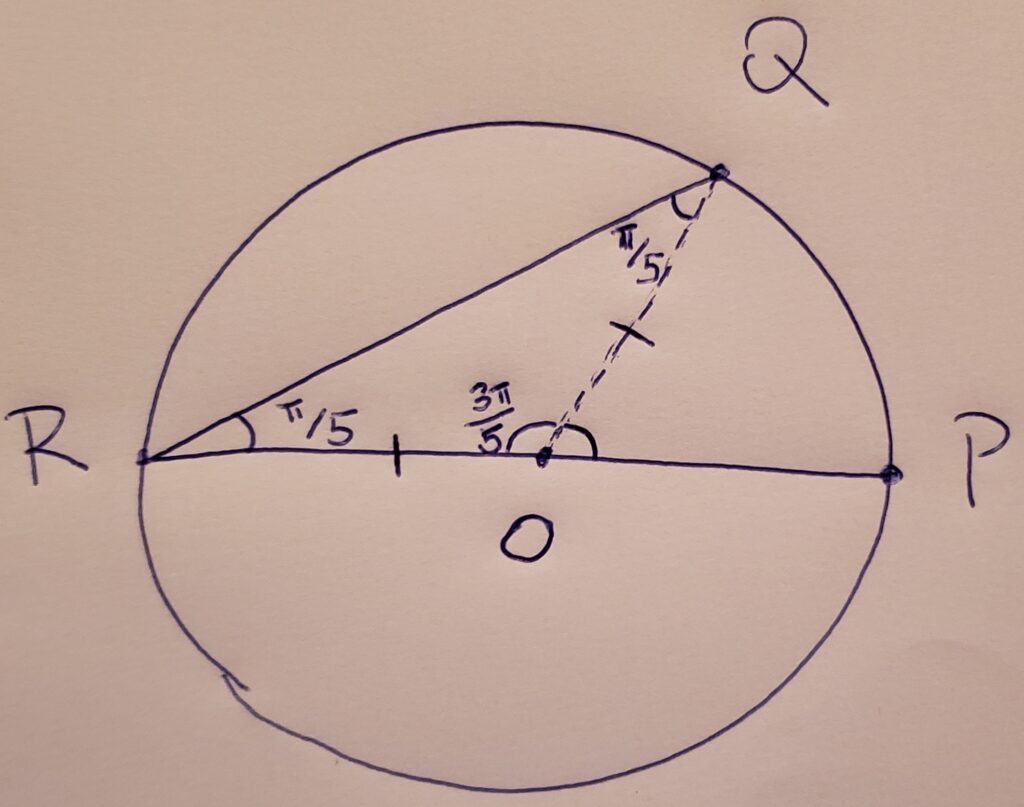
Dica 3:

Sabendo que o ângulo ROQ vale 3π/5 radianos, quanto vale o ângulo POQ?

Resolução da Dica 3:

Se juntarmos os ângulos ROQ e POQ, nós temos um segmentos. Logo a soma desses dois ângulos vale 180 graus.

ROQ + POQ = 180 graus

Mas, 180 graus é equivalente a π radianos. Logo,

ROQ + POQ = π radianos

Já calculamos que ROQ = 3π/5 radianos. Então

3π/5 + POQ = π

<=> POQ = π – 3π/5

<=> POQ = 5π/5 – 3π/5

<=> POQ = 2π/5

Dica 4:

Calculamos que o ângulo POQ vale 2π/5 radianos. Com essa informação, você pode calcular o comprimento do arco PQ.

Resolução da Dica 4:

O comprimento da volta completa de um círculo de raio r é 2.π.r.

O raio do círculo é de 0,3 km. Então o comprimento da volta completa do círculo mede 2.π.0,3 = 0,6π km.

Sabemos também que o ângulo de uma volta completa mede 2π radianos.

Agora, a gente pode concluir o exercício usando uma regra de três.

Uma volta completa (ângulo de 2π radianos) mede 0,6π km. O ângulo POQ mede 2π/5 radianos, então quanto vale o arco PQ?

Vamos chamar de y o comprimento do arco PQ. Agora, podemos aplicar a regra de três.

Regra de três:

2π radianos ~ 0,6π km
2π/5 radianos ~ y km

2π.y = 2π/5 . 0,6π

<=> y = 1/5 . 0,6π

<=> y = 0,6π/5 = 0,12π

Então, chegamos na resposta! O arco PQ mede 0,12π km

Resposta

Alternativa D